Como tirar (quase) qualquer conclusão a partir de um conjunto de dados? Como a Ciência de Dados determina se um experimento é significativo ou não? É possível atingir a neutralidade ou o fator humano pode interferir na conclusões de um experimento?
Ciência e Estatística
Antes que os conspiradores de plantão levantem uma lista de como a indústria farmacêutica é capaz de descobrir uma aplicação nova para a aspirina, ou decidir se o ovo faz bem ou mal para a saúde, posso ir adiantando que a história tem sua contraparte verdadeira, mas não será o assunto comentado neste texto. Sim, é possível usar a estatística para demonstrar (quase) qualquer coisa a partir de um conjuntos de dados, mas não vou elucidar o que pode ser feito de errado e nem analisar teorias conspiratórias. Meu objetivo, em termos gerais, é demonstrar como os cientistas usam a estatística para “provar”, “refutar” ou “não refutar” uma hipótese e como muitas vezes isso não é suficiente para tornar os resultados de um experimento realmente significativos, em seu sentido mais amplo. Isto é, embora busque demonstrar quais os elementos essenciais para que um experimento científico possa ser considerado significativo, comentarei algumas possíveis limitações da interpretação estatística, mostrando que variáveis ocultas e relevantes podem estar presentes.
Thomas Kuhn – que deu uma nova acepção à palavra “paradigma” quando escreveu “A Estrutura das Revoluções Científicas”, um dos mais citados livros de toda a história da ciência – costumava afirmar que a ciência não é apenas a busca racional por uma verdade “lógica”, algo como uma marcha lenta, progressiva e, por que não dizer, tediosa até um destino certo, mas também é o produto do próprio meio onde ela é produzida. Isto é, a ciência depende também das relações sociais, ambições, modismos, pressões que os cientistas sofrem por seus pares, e até pela sociedade como um todo. Afinal de contas, a profissão de cientista – atualmente tão combatida e questionada – deixou de ser apenas uma atividade para aqueles que desfrutavam de tempo e recursos financeiros, como era comum aos filósofos da antiguidade até o século XVIII, quando a revolução científica elevou a condição de “pensador(a)” a um novo patamar, até que se tornasse realmente uma profissão, a partir da chamadas revoluções industriais dos séculos seguintes.
A partir da profissionalização do cientista, questões comuns aos trabalhadores e trabalhadoras das fábricas começaram também a ser aplicadas aos profissionais da ciência, em que cumprir horários, metas e planos, bem como desenvolver pesquisas, escrever sobre elas e comunicá-las ao mundo começou a se tornar cada vez mais necessário. É o popular publish or perish (publique ou pereça), da expressão estadunidense, que sintetiza o modo atualmente dominante de se pensar o trabalho do cientista.
Natural, portanto, que um ramo de trabalho que se mostrou fundamental para o progresso econômico mundial – uma vez que a pesquisa científica e seus produtos tecnológicos têm sido os principais motores da economia global no século XXI – seja influenciado por diversos fatores além da mera busca pela verdade. Um desses fatores é, justamente, a necessidade constante de sistematização do “método científico”, em que se busca demonstrar a veracidade de determinada hipótese ou validar experimentos a partir de ferramentas matemáticas, como a estatística.
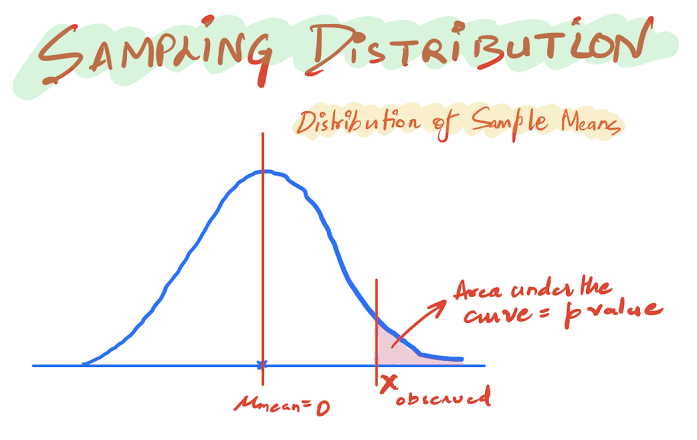
Há algum tempo atrás, encontrei uma matéria interessante da revista Nature que se dedicava à analise de um simples parâmetro, chamado valor-p, que é um conceito bastante conhecido em Data Science ou Ciência de Dados. A Ciência de Dados é um ramo eminentemente estatístico da computação que permite o trabalho com grandes volumes de dados e tem propiciado uma verdadeira revolução na era dos algoritmos de Inteligência Artificial. O valor-p é, basicamente, um parâmetro estatístico que indica se determinada hipótese, formulada a priori, deve ser rejeitada ou não. Por exemplo, como podemos testar a seguinte afirmação: uma xícara de café melhora o desempenho de estudantes antes das provas?
Um problema como esse pode ser formulado de acordo com duas hipóteses, que chamarei aqui de $H_0$ e $H_1$, hipótese nula e hipótese alternativa, respectivamente. Isto é, podemos formular o seguinte teste:
H0: "café não melhora o desempenho após uma xícara";
versus
H1: "café melhora o desempenho dos alunos".
As duas hipóteses podem ser verificadas a partir de determinados testes estatísticos, como o famoso teste t de Student, que gera o chamado “valor-p” como um dos parâmetros de decisão. Não irei detalhar a técnica em si, mas me concentrar no valor-p especificamente.
Se esse valor-p for pequeno – e este é usualmente considerado pequeno quando menor que 5% – considera-se que há uma pequena chance de a explicação ` café melhora o desempenho dos alunos` seja devida ao acaso. Isto é, se $p<5\%$, pode-se rejeitar a hipótese nula (para um nível de significância de 5%) e adotar a hipótese alternativa, que indica que o café melhora o desempenho dos estudantes.
Se o valor p for grande, ou seja, se $p>0,05$, o resultado do teste é inconclusivo, isto é, não se pode afirmar, dentro do nível de significância, que a hipótese $H_0$ seja verdadeira, ou, em outras palavras, não se pode afirmar que o café não melhora o desempenho dos estudantes. Até aí tudo bem, certo? Alguém consegue detectar um problema?
Bem, o problema com certeza não está no resultado do teste em si, mas reside na crença quase absoluta de que o conceito do p-value – que pertence a uma tradição de pensamento na estatística chamada de “frequentista” – seja correto para a tomada de decisões, como atestar se determinada descoberta, como no exemplo do café, pode ser considerada realmente significativa.
Além disso, em um teste estatístico, como num teste randomizado – muito comum em testes com seres humanos – considera-se que as hipóteses são sempre estabelecidas antes da coleta dos dados, isto é, parte-se de uma premissa de que os dados são coletados “às cegas”, o que nem sempre acontece. Por exemplo, se pretendemos comprovar a eficácia de uma nova droga no tratamento de uma doença, escolhemos um grupo de pessoas que vai tomar o medicamento e outro grupo, chamado grupo de controle, que tomará apenas uma pílula de açúcar, chamada de placebo. Em testes desse tipo, nem os próprios aplicadores dos medicamentos sabem para qual grupo estão sendo destinados determinado tipo de droga, e, em muitas ocasiões, não têm a menor ideia de que se está realizando uma pesquisa desse tipo. Após a coleta, seguem-se os testes estatísticos que geram parâmetros como o valor-p, que servem para validar a eficácia do método ou não.
O caso da crença no valor-p e, mais ainda, no intervalo de $5\%$ para o que é chamado “nível de significância” de uma descoberta é, precisamente, o assunto abordado pelo artigo da Nature, o que comento aqui. Alguns cientistas tem razões para acreditar que há um equívoco na interpretação e no uso indiscriminado do conceito, o que pode levar, inclusive, a uma taxa maior de “falsas descobertas”, supondo uma pesquisa idônea.
Por exemplo, o famoso e combatido (ex-)biólogo da Royal Society, Dr. Rupert Sheldrake, criador da Teoria da Ressonância mórfica (na qual as próprias leis da física podem também evoluir mais como hábitos do que como princípios fixos e imutáves), afirma ter desenvolvido um experimento simples para confirmar a antiga crença, compartilhada por muitas culturas, de que as pessoas sabem quando estão sendo observadas. O mais interessante das observações de Sheldrake, em nosso contexto, não são necessariamente afirmações em si, mas suas conclusões. Segundo as recomendações do controverso cientista, ao fazer uma coleta idônea de dados e realizar um teste de hipóteses, é possível encontrar um valor-p que rejeita a hipótese de que esses fenômenos (tidos como “paranormais”) não sejam possíveis, isto é, o autor afirma que é possível demonstrar, dentro do nível de significância, que a maior parte das pessoas sabe, de alguma forma, quando está sendo observada “por trás”, sem que esteja olhando diretamente. E mais, o nível de significância e a média de acertos é, segundo suas afirmações e de outros pesquisadores que replicaram o experimento, similar à média das observações do Bóson de Higgs!
Mas, peraí: por que o experimento do CERN – ao afirmar ter detectado o Bóson de Higgs, abriu caminho para o prêmio Nobel a François Englert e Peter Higgs – foi considerada como uma (grande) e genuína descoberta, enquanto que o experimento psicológico de Sheldrake não foi sequer considerado como relevante? Fica a pergunta…
Vale lembrar que o valor-p é somente a ponta de um grande iceberg.
